Introduction to Integral trees
The “Integral Tree” is a data structure proposed at Miltiadou et al, 2021 (https://www.mdpi.com/2072-4292/13/4/559/htm). It takes properties relating to “Integral Images” and embeds them into a tree structure. An “Integral Tree” consists of two elements: an integral 1D-array and
a tree. During the construction of the data structure, the node values
are arranged inside an 1D-array such that the node values of each branch are adjacent. Once the values are arranged, the 1-D array is
converted to integral. In the associated tree structure, each node
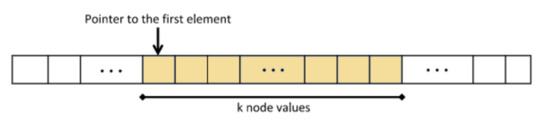
contains two parameters (*p,k). . At node N, the number k is the number of non-empty nodes that exist in the branch with root the node N. The pointer *p points to its first node value within the associated integral 1D-array (Figure 1).
Figure 1.
Ordering of tree elements.
This new Integral Tree data structure can be applied to binary trees, quadtrees and octrees. To
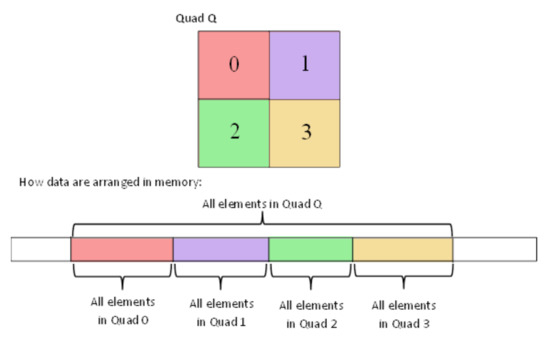
better perceive how this data structure works, Figure 2 gives an illustrative example of an integral quadtree. In order to build an integral quadtree the space should be recursively subdivided and the items of in the 1D array should be re-arranged at each recursion. Figure 2 shows how the
corresponding node values can be stored into the 1D-array in order to
fulfil the adjacency condition of the Integral Quatree.
Figure 2.
Illustration of how to save the values of an “Integral Quad Tree” into
the 1D-array, in order to preserve the condition of “Integral Trees”.
Integral Binary Tree Example
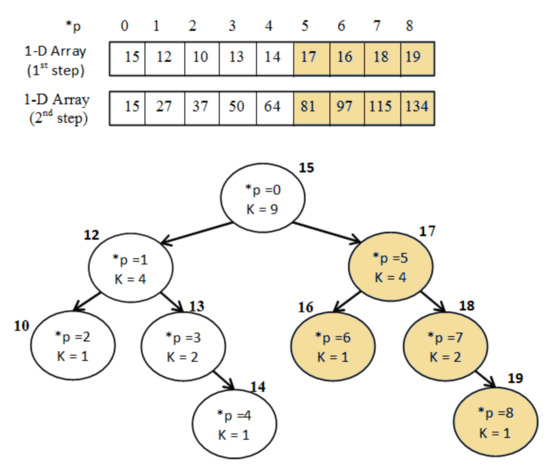
An example of a Binary Integral tree is given in Figure 3.
Figure 3.
Example of “Integral Binary Tree”.
At first, the values of the binary tree are sorted into the 1D-array A as {15,
12,10,13,14,17,16,18,19} in order to fulfil the adjacency condition. Secondly, the array
A is modified as
{15, 27,37,50,64,81,97,115,134} in order to become integral using the following equation:
Then the sum S of a branch, with (*p, k) parameters, is calculated at constant time as follows:
For instance, the sum of the yellow branch in Figure 3 is A[5+4−1]−A[5−1]=A[8]−A[4]=134−64=70
, which is correct since
17+16+18+19=70.
For more information on how to use Integral Octrees for surface reconstruction of implicit objects using the Marching cubes algorithms please refer to the related article:
https://doi.org/10.3390/rs13040559
Acknowledgement
This text has been modified from the following publication:
Miltiadou, Milto, et al. "A
comparative study about data structures used for efficient management of
voxelised full-waveform airborne lidar data during 3d polygonal model
creation." Remote Sensing 13.4 (2021): 559.
No comments:
Post a Comment